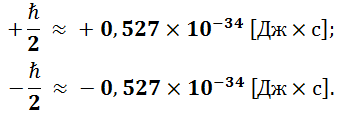Шаг назад

 

Глава 1. Постановка задачи

Перед тем, как приступить к обсуждению главной темы, поговорим о том, что же мы, собственно, собираемся измерять.

В некоторых опытах квантовые объекты ведут себя непредсказуемо. Продемонстрируем это на примере измерения момента импульса (спина) протона. Не сильно углубляясь в пучины теоретический механики, освежим в памяти, что такое вообще момент импульса. Для начала мы поговорим о классической величине.

Момент импульса характеризует вращательное движение физического тела вокруг некоторой точки пространства или вокруг некоторой оси. Нас будет интересовать ситуация свободного вращения тела вокруг собственной оси. Математически собственный момент импульса выражается вектором трёхмерного пространства. Длина (абсолютная величина) вектора находится в прямой пропорции с угловой скоростью и связана, таким образом, с интенсивностью вращения. А направление вектора момента импульса в пространстве совпадает с направлением собственной оси с учётом правила буравчика. Скажем, для юлы, вращающейся против часовой стрелки, вектор момента импульса считается направленным вверх.

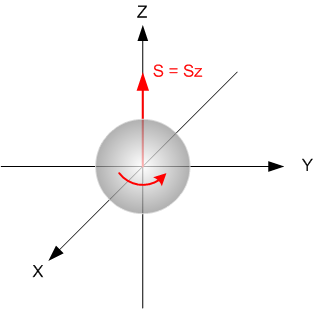
Поскольку момент импульса - это вектор, то он имеет разные проекции на разные направления в пространстве. Возьмём, например, классический шарик, вращающийся вокруг координатной оси Z против часовой стрелки.

Рисунок 1-1

Центр шара совмещён на рисунке с центром системы отсчёта. Шар как бы прозрачный такой, чтобы не загораживать прочие построения. 

Направление вектора S момента импульса в этом случае совпадает с направлением оси Z. А величина проекции спина на ось Z равна абсолютной величине вектора. Проекции на оси X и Y, само собой, нулевые, ведь никакого вращения вокруг этих осей не происходит.

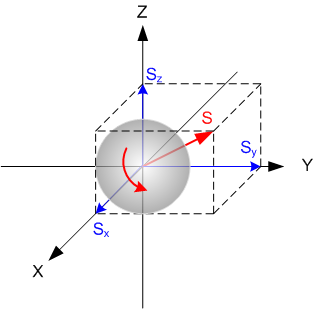
Теперь допустим, что тело вращается относительно другого направления, не совпадающего с координатными осями. Вот так, например:

Рисунок 1-2

Такой момент импульса имеет ненулевые проекции на все три оси X, Y, Z. Можно взглянуть на это дело и по-другому: вектор S относительно собственной оси вращения складывается из векторов - проекций S_x, S_y, S_z  на оси X, Y, Z.

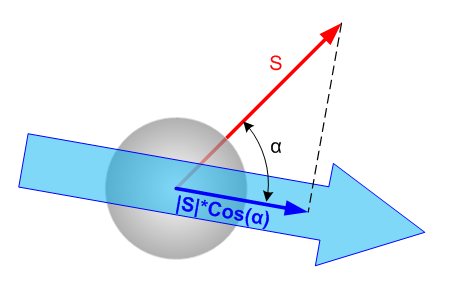
Всё это я к тому, чтобы плавно перейти к измерению момента импульса. Любой измеритель имеет собственное выделенное направление – ось прибора. Измеряется проекция момента импульса именно на это направление, так что результат измерения зависит от взаимной ориентации вектора S и оси прибора. Если мы измерим спин прибором, ось которого направлена так же, как вектор S, то мы получим максимальное положительное значение. Если ось прибора направлена противоположно S – будет максимальное отрицательное значение. Если же прибор ориентирован перпендикулярно S, то мы получим нулевое значение. Для произвольной ориентации результат измерения будет пропорционален косинусу угла между направлениями S и оси прибора.

Рисунок 1-3

На рисунке вектор момента импульса показан красной стрелкой, а направление прибора – толстой голубой стрелкой. Синяя стрелка – проекция спина на ось прибора.

Понятное дело, измерение одной проекции не даёт полной информации о моменте импульса, как измерение одной координаты не даёт полной информации о положении тела в трёхмерном пространстве. Не беда, можно просто измерить три разных проекции и построить из них вектор S. Пока, напоминаю, мы говорим о классическом моменте импульса и подразумеваем, что измерение не оказывает влияния на измеряемую величину. Или оказывает, но настолько мизерное, что им можно пренебречь.  

Переходим к измерению момента импульса протона. Пусть у нас есть источник одиночных протонов и прибор, способный измерять момент импульса попадающей в него частицы. Мы как-то ориентируем прибор в пространстве, пропускаем через него протон и получаем некое положительное или отрицательное число – значение момента импульса, точнее говоря, значение проекции момента на ось прибора.

Договоримся о «языке»

В наших опытах мы будем проводить серии однотипных измерений. Одно измерение назовём «выстрел», имея в виду генерацию протона, запутанной пары или запутанной тройки и последующие манипуляции с ними. А наблюдаемые последствия одного выстрела будем называть исходом. Результатом же будем называть обобщённые данные эксперимента по всей серии выстрелов, а также любой логический вывод наших рассуждений.

Что мы ожидаем увидеть? Мы не знаем, с каким моментом импульса  генерируются протоны, поэтому предполагаем, что исход измерения будет случайным. То есть, в результате серии измерений – несколько выстрелов с разной ориентацией прибора – мы ожидаем получить более-менее равномерное распределение исходов с центром в нуле. Однако на практике получается совсем другое. При таком измерении мы в каждом выстреле получаем только одно из двух значений: 

 Здесь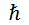– постоянная Дирака (она же – приведённая постоянная Планка), приблизительно равная .  

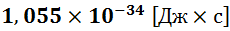Замечание

Обратите внимание на примечательный факт: постоянные Планка и Дирака измеряется в тех же единицах, что и момент импульса – Джоуль умножить на секунду.

Довольно странно, правда? Оказывается, что момент импульса протона при измерении квантуется. Как бы мы не крутили прибор, можем получить лишь один из двух исходов.

Этот результат существенно отличается от того, который мы получали бы для обычного вращающегося шарика. Выходит, исход измерения определяется не классическим вращением, а неким иным свойством частицы. Мы назовём это особое свойство – «спин». Физический смысл этого свойства вам объяснить никто не сможет  – «науке это не известно». Но несколько вполне достоверных утверждений по поводу спина сделать можно. Вот первое, в справедливости которого мы уже убедились на опыте:

Утверждение 1. Спин протона делает невозможным при измерении момента импульса получить какой-либо иной исход, кроме 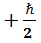 или .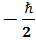

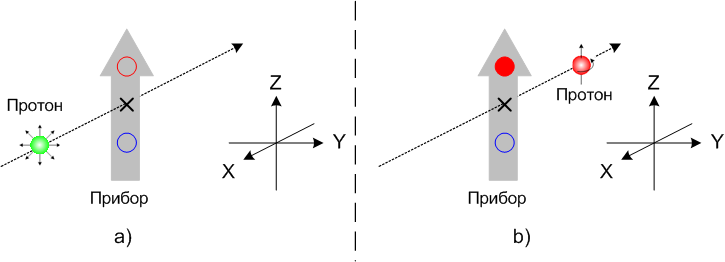
Поскольку допустимых исходов всего два, дальше мы можем «забыть» про абсолютные значения момента импульса. Примем величину 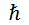 за единицу и будем говорить, что возможны только два исхода: «спин плюс одна вторая» и «спин минус одна вторая». А можно и того короче: исходы «плюс» и «минус». Дальше на рисунках мы будем изображать наши опыты очень схематично, вот так:     

Рисунок 1-4

На каждой из этих картинок показан протон и сам прибор в виде толстой серой стрелки с двумя датчиками. Срабатывание красного датчика означает исход выстрела «плюс», синего – исход «минус». На левом рисунке ситуация перед измерением – не один датчик пока не сработал (пустые кружочки). На правом рисунке ситуация после измерения – исход «плюс» (красный кружок закрашен), протон вышел из прибора. Дополнительно на рисунках показана система координат, чтобы было, к чему привязаться при объяснении. В данном случае прибор сориентирован вдоль оси Z. Но это, понятное дело, произвольный выбор, мы могли бы начать наши опыты с любого другого направления, на результат это не повлияло бы – те же два исхода.   

В попытке дать классическое объяснение полученного результата можно предположить следующее: а если прибор измеряет не момент импульса, а какой-то другой параметр? О природе этого параметра нам пока ничего не известно, он для нас «скрытый». Мы предполагаем только, что этот икс-параметр определяет исход измерения на приборе и носит бинарный характер, то есть, может принимать только два значения, условно «плюс» и «минус». Для сравнения: бинарной величиной является также элементарный электрический заряд. 

Воодушевившись таким предположением, проведём следующий опыт.

 

Рисунок 1-5

 

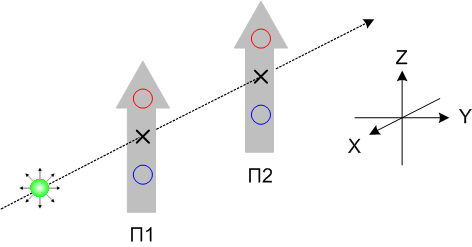
Теперь мы дважды измеряем один и тот же протон при неизменной ориентации прибора.

Определение

Ориентацию прибора дальше будем называть «измерительным базисом» или просто «базисом». Например, фраза «измерение в Z-базисе» будет означать то же самое, что и «измерение прибором, ось которого направлена по координатной оси Z». Рисунок 1-5 иллюстрирует ситуацию, когда мы дважды измеряем протон в Z-базисе.

Проведём серию выстрелов и обнаружим, что приборы П1 и П2 всегда срабатывают синхронно: либо оба выдают «плюс», либо оба «минус». Это, казалось бы, подтверждает идею о существовании икс-параметра. Если бы прибор выдавал исход, не зависящий от внутренних свойств протона, то такой синхронности мы бы не наблюдали. А поскольку наблюдаем, то можем уверенно сказать: протон, измеренный в базисе П1, несёт в себе «программу», однозначно предопределяющую исход следующего измерения в таком же базисе.

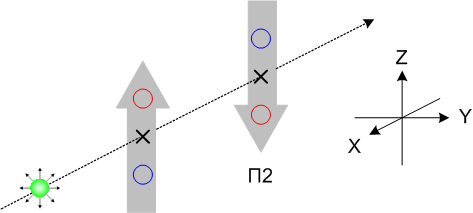
Теперь измерим один протон в двух противоположно ориентированных базисах. Пусть П1 ориентирован по оси Z – «вверх», а П2 – по той же оси – «вниз».

Рисунок 1-6

 

В таком опыте исходы на П1 и П2 всегда противоположны, если на одном «плюс», то на другом непременно «минус», и наоборот. Таким образом, если для какого-то базиса икс-параметр предопределён, то для базиса, развёрнутого на 180 градусов он предопределён тоже, но обратным образом.

Результаты опытов 1-5, 1-6 позволяют нам сделать очередное утверждение о свойствах спина:

Утверждение 2. Исход измерения может быть однозначно предопределён относительно некоторого базиса.

Точнее говоря, даже относительно двух базисов: «прямого», в котором предопределён исход «плюс», и «обратного», в котором предопределён «минус».

Теперь мы можем договориться о таком понятии, как направление спина. Будем считать, что это направление совпадает с таким приборным базисом, в котором однозначно предопределён результат измерения «плюс».  Как видите, это совсем не то же самое, что мы имели в виду, говоря о направления вектора классического момента импульса.

Дополнительное пояснение к рисунку 1-4

Сразу после генерации, до попадания в прибор, направление спина не определено (в концепции детерминизма – неизвестно), что обозначено кучей торчащих из протона зелёных стрелочек. А на выходе из прибора, при исходе «плюс», направление спина совпадает с направлением координатной оси Z. При исходе «минус» направление спина было бы, ясное дело, противоположно.

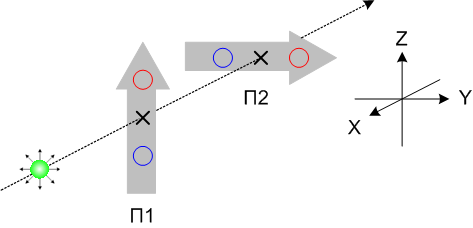
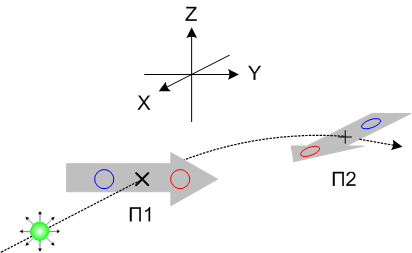
Экспериментируем дальше. Попробуем измерить один протон в двух перпендикулярных базисах. Пусть П1 ориентирован по оси Z, а П2 – по оси Y.

Рисунок 1-7

В такой конфигурации никакой синхронности уже не будет, все четыре комбинации исходов мы будем получать с одинаковой вероятностью. Тот же результат мы получим, если первое измерение проведём, например, в Y-базисе, а второе – в X-базисе:

  

Рисунок 1-8

 

Побочное замечание

У кого-то может возникнуть вопрос: каким образом мы в опыте 1-8 изогнули траекторию протона между П1 и П2? Технически это сравнительно просто сделать с помощью электрического или магнитного полей. Причём так, чтобы спиновое состояние протона не менялось при перемещении его от П1 к П2.  Так что пунктирную линию со стрелкой предлагаю считать не столько обозначением траектории протона, сколько обозначением последовательности измерений в одном выстреле. В принципе, мы вообще могли бы обойтись одним прибором, поворачивая его перед каждым измерением так, как нам надо, и запуская в него тот же протон.    

Созрело

Утверждение 3. Если направление спина перпендикулярно базису прибора, то исход совершенно непредсказуем.

Продолжая размышлять в рамках классического детерминизма, выдвигаем следующее предположение: ещё до входа в П1 в протоне уже «прописан» исход измерения для любого базиса.

Чуточку философии

Это означает, что любой протон несёт в себе «файл», где для каждой ориентации прибора записано значение икс-параметра. Поскольку количество возможных измерительных базисов бесконечно, то такой «файл» должен содержать в себе бесконечное количество информации. Это довольно сомнительно, согласитесь.

В опыте 1-7 на П1 мы выясняли икс-параметр для Z-базиса, на П2 – для Y-базиса. Далее мы как будто бы можем измерить тот же протон при прочих ориентациях прибора и установить значение икс-параметра для любого измерения. Что же, идея на первый взгляд может показаться здравой. Но она не работает, потому что:

Утверждение 4. У протона на выходе из прибора направление спина совпадает с базисом при исходе «плюс» либо противоположно базису при исходе «минус».

Иными словами, измерение меняет спин протона в согласно полученному исходу. Кроме, конечно, тех двух случаев, когда ещё до измерения направления спина и базиса совпадают либо противоположны.

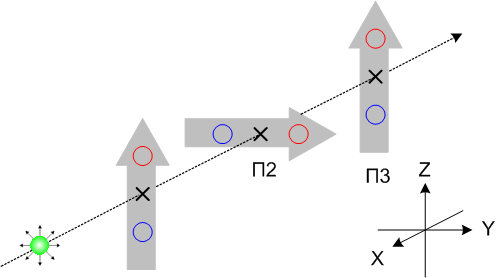
Убедиться в справедливости утверждения 4 нам поможет следующий опыт.  

Рисунок 1-9

Всё просто: если, как мы предположили, спин при измерении не меняется, то исходы приборов П1 и П3 должны всегда совпадать, как было в опыте на рисунке 1-5. Но это не так, примерно в половине попыток приборы П1 и П3 будут давать противоположные исходы. Стало быть даже если на входе П2 спин протона определён относительно Z-базиса, то на выходе П2 уже не определён. Таким образом, измерение в Y-базисе на П2 меняет состояние протона, причём, меняет необратимо. Следовательно, с мечтой установить изначальную программу протона методом нескольких разнобазисных измерений мы можем распрощаться. Практический вывод: невозможно одновременно измерить спин, или, если угодно, икс-параметр, в двух разных базисах.

Однако, невозможность установить программу ещё не означает, что её нет. Вот тут как раз сталкиваются классический консерватор и квантовый новатор.   

Сторонники классического детерминизма утверждают, что исход измерения спина относительно направления Y, как и относительно любого другого направления, тоже предопределён однозначно. В опыте 1-7 мы после первого измерения знаем икс-параметр для Z-базиса. Но не знаем его для Y-базиса, для нас это «скрытый параметр». Но он есть, в не зависимости от нашего о нём знания.   

Сторонники квантовой неопределённости возражают: в данном случае исход действительно предопределён относительно Z-базиса. Но относительно Y-базиса предопределения нет, существуют две альтернативы и выбор между ними абсолютно случаен, никакой программы на этот счёт в протоне не существует.

Вот это мы и будем выяснять, существует программа или нет.

 

Шаг вперёд