Глава 2. ЭПР-пары и ГХЦ-тройки
Как нам подступиться к задаче, поставленной в первой главе? Действительно, мы не можем прямо измерить две разных проекции спина у одной частицы. Но можем сделать более хитро: изготовить пару скоррелированных частиц. Теоретически это можно сделать так. Предположим, у нас есть частица со спином единица (за единицу, напомню, мы приняли значение постоянной Дирака). Пусть эта частица самопроизвольно распадается на две идентичных частицы, условно - частицы A и B. Спин, поскольку он есть квантовый аналог момента импульса, подчинятся закону сохранения, а значит, суммарный спин частиц A и B тоже должен быть единичным. Следовательно, спины частиц A и B равны между собой и равны одной второй. Более того, они совпадают по направлению. Таким образом, мы с вами получили то, что физики называют ЭПР-парой.
Здравый смысл подсказывает, что если мы измерим момент импульса обеих частиц, в одном (любом!) базисе, то мы получим одинаковый исход, иное закон сохранения момента импульса запрещает. Что же, раздобудем где-нибудь источник ЭПР-пар и проведём опыт, измерив оба протона в одном базисе.
|
|
|
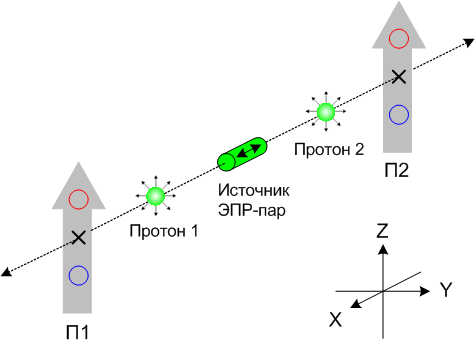
Рисунок 2-1 |
Так и есть, при одинаковой ориентации приборов исходы измерений на П1 и П2 всегда находятся в стопроцентной корреляции. Казалось бы, этот факт свидетельствует в пользу детерминистов. Но у сторонников принципиальной неопределённости другое мнение. Представим себе типичную дискуссию об этом опыте между классическим физиком (CP) и квантовым механиком (QM).
CP: Если бы исход для каждой частицы был случаен, то совпадение результатов в каждой из множества попыток было бы невозможно. Значит, «программа» есть, и в данном случае она одинакова у обеих частиц ЭПР-пары. Поэтому мы можем измерить протон 1, например, в Z-базисе и узнать икс-параметр для направления Z. А протон 2 - измерить, скажем, в Y-базисе и узнать программу для направления Y.
QM: исход действительно случаен, но только для первого измерения. Мы не можем рассматривать ЭРП-пару как две независимых частицы, это единая квантовая система. Измерения одной из частиц влияет на состояние всей системы в целом. В данном случае измерение одной частицы изменяет состояние второй частицы так, как будто она сама подверглась такому же измерению и с таким же исходом. Например, пусть первым срабатывает плюс-датчик П1. Тогда состояние протона 2 изменяется таким образом, как будто она сама попала в П1 и дала исход «плюс». Таким образом, для прибора П2, ориентированного также, как и П1, спин протона 2, становится определённым, а исход будущего измерения безальтернативным: частица гарантировано даст «плюс». Поэтому ваше предложение не годится. Как только мы измерили один протон, состояние второго тут же меняется. Это не даёт нам возможности узнать изначальную программу для перпендикулярных базисов. Впрочем, никакой программы, то есть, никаких параметров, предопределяющих исход, в частице нет. Но есть параметры, предопределяющие вероятность того или иного исхода.
CP: По вашему выходит, что между частицами ЭПР-пары существует какой-то канал связи, по которому исход первого измерения передаётся второй частице. Это представляется весьма сомнительным!
QM: Действительно, такая «связь» есть. Только мы называем её по-другому: «квантовая запутанность».
CP: Пусть частицы ЭПР-пары разнесены очень далеко друг от друга, например, одна на Земле, вторая – на другом краю галактики. И пусть оба измерения производятся примерно в одно и то же время. В таком случае обмен информацией между частицами за время от первого измерения до второго невозможен, ведь сигнал от одной частицы до другой, согласно теории относительности, будет идти десятки тысяч лет. Хотите сказать, что при такой постановке эксперимента корреляции уже не будет?
QM: Корреляция будет. Дело в том, что никакого в буквальном смысле «сигнала» не существует, здесь взаимодействие совершенно другого рода. Оно распространяется мгновенно и без всякого физического носителя. Однако, предвидя ваши возражения, сразу оговариваю: теории относительности это не противоречит и ни к каким нарушениям причинности не приводит. Этим взаимодействием нельзя воспользоваться для мгновенной передачи настоящего сигнала. Потому что, хотя корреляция и имеет место, но сам факт этого можно установить лишь после того, как наблюдатели свяжутся между собой по обычному классическому каналу и сверят свои исходы.
CP: Хм... Возможно, ваша запутанность и не нарушает принципа причинности. Но она нарушает принцип локального реализма и подразумевает «пугающее дальнодействие»!
QM: Да, нарушает. Что же, в науке случается и такое, иногда приходится пересматривать базовые принципы. Скажем, до Эйнштейна считалось, что время абсолютно и течёт одинаково во всех системах отсчёта. Да и ограничения на скорость не было, полагали, например, что гравитационное взаимодействие распространяется мгновенно. Но теория относительности эти взгляды отменила.
CP: Как угодно, но ваша квантовая механика слишком радикальна. Да, пусть она безупречно предсказывает результаты серий экспериментов с частицами. Но она противоречит принципам детерминизма и локального реализма, значит, квантовая механика в чём-то неверна или, как минимум, неполна. Геоцентрическая система с её эпициклами тоже согласовывалась в своё время со всеми известными наблюдениями и претендовала на звание истинной картины мира. Но потом появились новые данные, и выяснилось, что это вовсе не физика, а голая математика. А вы даже картины мира не даёте, одну математику. Сами же, когда вас просят объяснить физический смысл квантовой механики, отвечаете: «заткнись и считай».
JB (в дискуссию вступает Джон Белл): Коллеги, возникла идея, как проверить, кто из вас прав. Надо многократно измерить спин частиц ЭПР-пар а разных базисах. Я тут посчитал и получается, что в некоторых комбинациях приборов «программа» и «дальнодействие» предсказывают разную статистику исходов.
Вот вам очень «краткая история» появления неравенств Белла. Как уже было сказано во введении, эксперименты по проверке этих неравенств были многократно проведены, и они статистически подтвердили существование дальнодействия. В экспериментах использовались те самые запутанные ЭПР-пары, которые называют также «белловские состояния». Гринбергер, Хорн и Цайлингер придумали, а позже реализовали более сложный эксперимент, который дал прямое (не статистическое) подтверждение дальнодействия. В этих опытах использовались уже не пары, а тройки запутанных частиц, так называемые ГХЦ-состояния.
Теперь мы готовы к тому, чтобы чётко сформулировать условия нашего эксперимента.
Условие 1. Имеется источник, который может в одном выстреле генерировать три протона в ГХЦ-состоянии. Условно обозначим эти протоны как A, B. С.
Условие 2. Мы разносим протоны тройки в разные места. Удобнее объяснить так: пусть в удалённых друг от друга местах имеется три экспериментатора, традиционно назовём их – Алиса, Боб и Чарли. Протон A мы отправляем Алисе, протон B – Бобу и протон C – Чарли. Важно: протоны мы перемещаем таким образом, чтобы их спин сохранялся.
Условие 3. Каждый экспериментатор может измерить спин своего протона относительно одного из трёх взаимно перпендикулярных направлений – X, Y, Z. Подразумевается, что системы координат Алисы, Боба и Чарли сориентированы в пространстве одинаковым образом.
Условие 4. Для каждого выстрела у нас будет собственный план измерений. Допустим, мы хотим, чтобы Алиса измерила спин своего протона относительно X, Боб – относительно Y, Чарли – относительно Z. Такой план мы обозначим как измерение 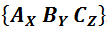 или измерение в
или измерение в 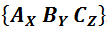 базисе. Вот так, в фигурных скобках. Если хотим, чтобы все трое измерили спин относительно Z, то это будет
базисе. Вот так, в фигурных скобках. Если хотим, чтобы все трое измерили спин относительно Z, то это будет 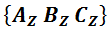 измерение, и так далее. Вот, например, иллюстрированная схема измерения в
измерение, и так далее. Вот, например, иллюстрированная схема измерения в 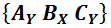 базисе:
базисе:
|
|
|
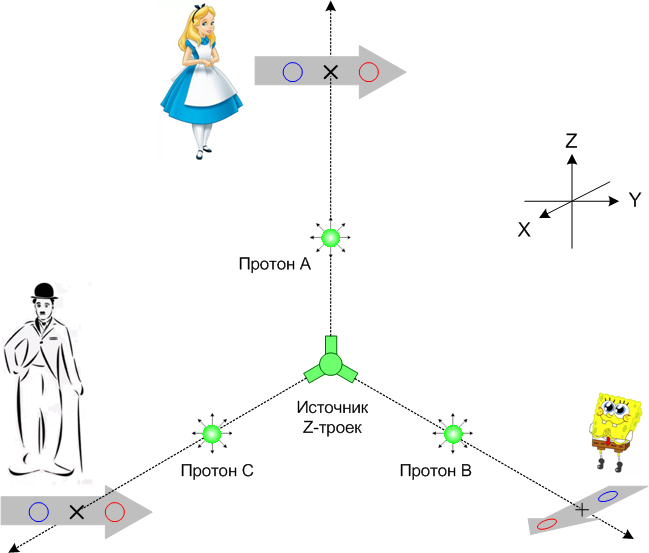
Рисунок 2-2 |
Теперь подробнее о ГХЦ-состояниях. Оказывается, тройку частиц можно сгенерировать таким образом, что исходы измерений Алисы, Боба и Чарли будут взаимно коррелировать. Вот такую коррелирующую тройку мы и будем называть ГХЦ-состоянием. Конкретно, пусть наш источник создаёт такую тройку, что все три протона дадут одинаковый исход при измерении в Z-базисе. То есть, либо все три «плюс», либо все три «минус». Такое ГХЦ-состояние будем называть «z-тройка».
Как практически получить z-тройки, мы тут разбираться не будем, просто поверьте, что это возможно.
Лабораторная практика
Описание реального эксперимента содержится в оригинальной статье (pdf, английский) на Figure 1. Там, правда, используются не протоны, а фотоны, но логики рассуждений это не меняет. Можно было бы раскрыть тему и на фотонах, конечно, но это вызвало бы дополнительные трудности. В частности, пришлось бы разбираться с тем, что такое "круговая поляризация".
Наша задача установить – чем обусловлена корреляция между протонами z-тройки – программой, которую несёт в себе каждый из протонов, или дальнодействием протонов при измерении.