Принцип 4 (окончание)
Важное замечание: QS всегда рассматривается относительно конкретного измерения. Физики это называют «представление квантового состояния». Например, если предполагается измерение координаты частицы, то описывают QS в координатном представлении. Причём, для каждой координаты своё: «QS в представлении координаты X», «QS в представлении координаты Y». Если измеряется импульс, QS исчисляется в импульсном представлении. Если энергия – в энергетическом, и так далее.
У нас, вот, выражения (f.4-1, f.4-2) – это QS протона в моментно-импульсном представлении относительно координатной оси Z. Оно же – 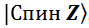 . На всякий случай напомню, что спин – это квантовое состояние, которое измерить нельзя. И когда говорят «измерение спина» – это не совсем точно. На самом деле измеряется всегда момент импульса. Но в квантовой литературе принято писать «измерение спина», ну и мы так будем.
. На всякий случай напомню, что спин – это квантовое состояние, которое измерить нельзя. И когда говорят «измерение спина» – это не совсем точно. На самом деле измеряется всегда момент импульса. Но в квантовой литературе принято писать «измерение спина», ну и мы так будем.
Различные представления одного и того же квантового состояния могут быть взаимозависимы. Например, координатное представление QS свободной частицы однозначно предопределяет импульсное представление.
Шаг в сторону
Самое знаменитая иллюстрация – всё тот же принцип неопределённости Гейзенберга. Чем лучше определена координата, тем хуже определён импульс, и наоборот. Если функция, описывающая зависимость амплитуды вероятности от координаты (это и есть QS в координатном представлении) выглядит, как узкий пик у какого-то значения координаты, то функция того же QS в импульсном представлении будет более-менее равномерно размазана в широком диапазоне значений импульса. И наоборот, что в импульсном – пик, то в координатном – плато.
Для наших задач важно то обстоятельство, что для спинового QS протона представления 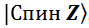 ,
, 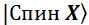 ,
, 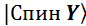 , а также
, а также 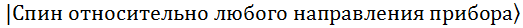 однозначно взаимосвязаны. Пусть, например, в Z-представлении частица находится в базисном состоянии
однозначно взаимосвязаны. Пусть, например, в Z-представлении частица находится в базисном состоянии 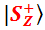 :
:
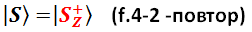
Для Z-измерения существует единственная перспектива с единичной амплитудой вероятности. Однако, если мы тот же протон представим в X-базисе, то будет уже суперпозиция двух равновесных перспектив:
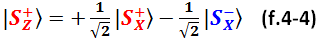
Это математическое описание обнаруженного нами ранее физического явления: если при измерении в Z-базисе исход предопределён, то при измерении в X-базисе никакой определённости нет, исходы «плюс» и «минус» равновероятны.
А вот так в X-базисе выглядит второе Z-базисное состояние «спин минус»:
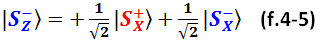
Запишем также Z-базисные состояния в представлении Y-базиса:
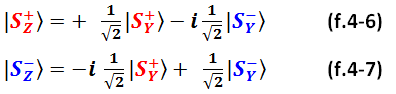
Преобразования (f.4-4 – f.4-7) нам пригодятся при анализе ГХЦ-состояний, поэтому прошу взять их на заметку.
Первоисточник
Формулы (f.4-4 – f.4-7) выведены с опорой на Фейнмановские лекции по физике, том 8, глава 4. Там используется правая система координат, и у нас тут тоже (рисунок 1-1).
X-базис соответствует повороту прибора вокруг оси Y на 90° против часовой стрелки (правый винт). Вот кусочек из Фейнмана для этого случая:
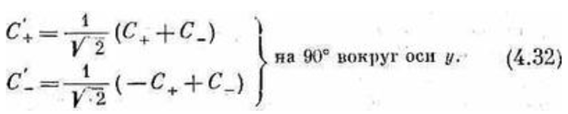
Здесь амплитуды X-представления 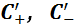 выражены через амплитуды Z-представления
выражены через амплитуды Z-представления 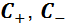 В наших обозначениях этому соответствует следующее:
В наших обозначениях этому соответствует следующее:
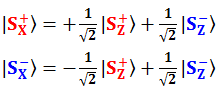
Мы, наоборот, выражаем Z–представление через X-представление и получаем формулы (f.4-4, f.4-5).
Y-базис соответствует повороту прибора вокруг оси X на –90°. Пользуемся вот этим:
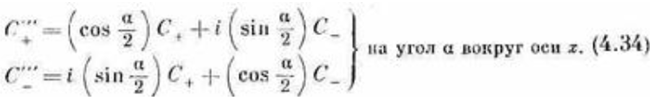
Аналогично, выражаем Z–представление через Y–представление и получаем формулы (f.4-6, f.4-7).
Прошу обратить внимание вот ещё на что. Если мы будем измерять состояния 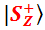 и
и 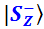 в X-базисе (f.4-4, f.4-5), то и в том, и в другом случае вероятность исходов «плюс» и «минус» будет одинаковой. Тем не менее, это разные состояния. В Z-представлении их отличие видно невооружённым глазом, протон в состоянии
в X-базисе (f.4-4, f.4-5), то и в том, и в другом случае вероятность исходов «плюс» и «минус» будет одинаковой. Тем не менее, это разные состояния. В Z-представлении их отличие видно невооружённым глазом, протон в состоянии 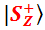 при Z-измерении однозначно выдаст результат плюс, а протон
при Z-измерении однозначно выдаст результат плюс, а протон 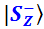 – однозначно «минус». А вот X-представления этих состояний отличаются знаком амплитуды вероятности перспективы
– однозначно «минус». А вот X-представления этих состояний отличаются знаком амплитуды вероятности перспективы 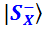 . В виду важности знаков амплитуд я буду писать их даже там, где обычно не принято, например, сразу после знака равенства, как в формулах (f.4-4 – f.4-7) или после открывающей скобки в некоторых следующих формулах.
. В виду важности знаков амплитуд я буду писать их даже там, где обычно не принято, например, сразу после знака равенства, как в формулах (f.4-4 – f.4-7) или после открывающей скобки в некоторых следующих формулах.
Те же рассуждения верны и для Y-представления (f.4-6, f.4-7): вероятности исходов одинаковы, но состояния разные, потому что разные амплитуды перспектив 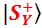 и
и 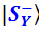 . При этом они отличаются не только знаком, но и тем, что одна амплитуда выражается действительным числом, а другая – мнимым. Тем не менее, модули всех амплитуд здесь одинаковы и равны
. При этом они отличаются не только знаком, но и тем, что одна амплитуда выражается действительным числом, а другая – мнимым. Тем не менее, модули всех амплитуд здесь одинаковы и равны 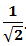 .
.
Надеюсь, мне удалось прояснить, как надо понимать формулы, выражающие спиновое квантовое состояние. Если же кто-то спросит, как они выведены, то этого вот так «на пальцах» не покажешь. Кто хочет узнать, тому придётся всё же освоить высшую математику и осилить уравнение Дирака вместе с его многочисленными следствиями. Нам же здесь достаточно осознания того, что эти формулы работают и вполне соответствуют экспериментальным результатам измерения спина протона в разных базисах, а также умения ими (формулами) пользоваться.
Реализованные планы
Как и обещал в предыдущем релизе этой статьи, выложил на сайт материал, в котором представлено вполне классическое устройство, поведение которого описывается точно такими же формулами, как и чистое квантовое состояние одиночного протона. Там показано: вся эта комплексная математика вовсе не является голой квантовой абстракций, а вполне применима и для некоторых классических расчётов.
Как раз в порядке усиления умения давайте посмотрим, как будет выглядеть в различных базисах произвольное квантовое состояние. Возьмём, например, то, которое мы уже записали выше, смотрите формулу (f.4-1). Сначала «перегоним» это состояние в X-базис. Дальше выписана цепь преобразований, а в разрывы цепи вставлены текстовые комментарии того, что мы делаем.
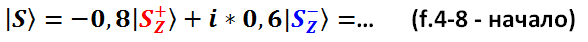
Вместо базисных состояний Z-представления 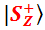 и
и 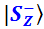 подставляем их X-представления – формулы (f.4-4, f.4-5):
подставляем их X-представления – формулы (f.4-4, f.4-5):
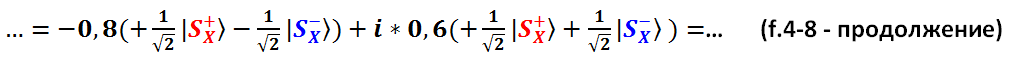
Раскрываем скобки – элементарная арифметика:
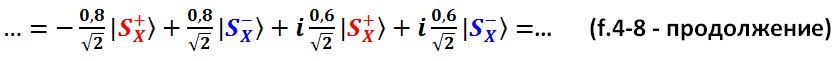
Склеиваем вместе разорванные «кусочки» векторов-перспектив 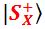 и
и 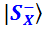 :
:
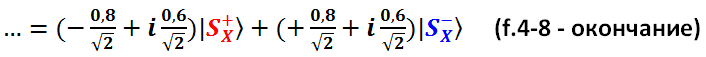
Готово. Можем сравнить модули амплитуд (сами амплитуды в скобках) и увидеть, что они одинаковые. Вероятности исходов «плюс» и «минус» при измерении спина состояния (f.4-1) в X-базисе тоже, значит, одинаковые.
Теперь посмотрим, как будет выглядеть состояние (f.4-1) в Y-базисе. Уже пишем без разрывов и комментариев:
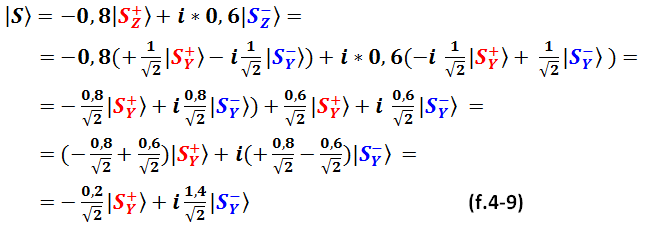
Шпаргалка
В преобразовании учтено то, что перемножение двух мнимых единиц равно действительной единице с минусом: 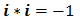
Как видим, при измерении в Y-базисе вероятности исходов уже различны: 0,02 для исхода «плюс» и 0,98 для исхода «минус». Проверьте!
