Принцип 4. Каждая перспектива характеризуется особой физической величиной – амплитудой вероятности. Эта величина математически выражается комплексным числом. Вероятность реализации перспективы при измерении равна квадрату модуля амплитуды.
Раз уж мы считаем перспективу реальным физическим объектом, то логично предположить, что она обладает реальными физическими свойствами, которые выражаются через математические величины. Например, движущееся тело обладает классическим импульсом, который выражается вектором трёхмерного пространства. Это данность, которую мы принимаем без доказательства, как постулат. Вот так же, как постулат, примите и то, что квантовая перспектива обладает амплитудой вероятности, которая выражается вектором двухмерной комплексной плоскости, или, что то же самое, комплексным числом. Годного классического аналога амплитуда вероятности, увы, не имеет. Однако, рискну предложить некоторые соображения, которые, надеюсь, помогут вам если не осознать, то хотя бы интуитивно почувствовать физический смысл этой величины.
Обратимся опять к лототрону. От чего зависит вероятность перспективы вытащить конкретный, например, красный цвет? Детский вопрос – от количества красных шаров в лототроне, конечно. Точнее, от отношения количества красных шаров к общему количеству шаров. Мы полагаем, что у каждого шара есть шанс быть вытащенным. Всего шансов столько, сколько шаров в лототроне. А у каждой перспективы вытащить тот или иной цвет столько шансов реализоваться, сколько имеется шаров этого цвета. Очевидное вещь, но обращаю ваше внимание на следующие не столь очевидные, но несомненные обстоятельства. Во-первых, мы по умолчанию полагаем, что каждый шар в лототроне обладает некоей физической величиной, которую навскидку можно назвать: «реализуемость». И даже присваиваем этой величине единицу измерения: один шанс. Во-вторых, мы считаем, что перспектива также обладает реализуемостью, которая определяется как сумма шансов по всем шарам, представляющим данную перспективу. В частности, реализуемость перспективы «красный» равна суммарному количеству «красных» шансов – количеству красных шаров. Суть этого пассажа: на вероятность случайного выбора даже в классическом случае влияет другое физическое свойство, та самая реализуемость. Но в классическом лототроне между реализуемостью и вероятностью прямая зависимость. Настолько прямая, что многие, наверное, даже не почувствуют тонкого различия между этими величинами.
Я не буду утверждать, что амплитуда квантовой перспективы – это то же самое, что мы тут назвали реализуемостью. Тем не менее, это родственные величины. Подобно тому, как реализуемость перспективы определяет вероятность классического выбора, амплитуда определяет вероятность квантового выбора. Но зависимость вероятности от амплитуды уже не линейная, а несколько более сложная. Тем не менее, попробуем с ней разобраться.
Перед тем, как двигаться дальше, договоримся о том, что мы будем называть квантовым состоянием. В целях борьбы с тавтологиями в дальнейшем тексте сократим «квантовое состояние» до QS (Qantum State). Так вот, QS – это совокупность всех перспектив, каждая со своей амплитудой вероятности. Пояснить смысл термина «квантовое состояние» удобнее не через прямое определение, а через способ описания. Говоря о конкретном QS, мы просто перечислим все перспективы и укажем амплитуду вероятности для каждой из них.
Модель
Так, описывая «вероятностное состояние» лототрона с шарами, мы бы сказали: вероятность вытащить красный шар – две третьих, вероятность вытащить синий шар – одна третья. Квантовое состояние описывается в аналогичных вероятностных терминах, с той лишь разницей, что амплитуда вероятности выражается в общем случае не положительным вещественным числом, как классическая вероятность, а комплексным.
Например, для спина протона, измеряемого в определённом базисе, мы могли бы перечислить и указать:
- амплитуда вероятности перспективы
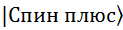 равна – 0,8;
равна – 0,8; - амплитуда вероятности перспективы
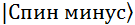 равна + i * 0,6;
равна + i * 0,6;
Справочка
В данном примере и дальше i – это комплексная единица. Как я уже предупреждал во введении, читателю последующей писанины желательно понимать, что такое комплексные числа. Хотя бы на том уровне, чтобы отличать модуль комплексного числа от его аргумента.
Всё, для описания спинового QS ничего больше не требуется, других перспектив при измерении спина протона не существует.
По ходу рассказа будем вводить обозначения, которые нам дальше понадобятся. Перспективы будем обозначать так 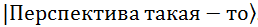 : Слева прямая скобка, справа – угловая, а между ними – идентификатор перспективы. А QS опишем как сумму всех перспектив, помноженных на свою амплитуду каждая:
: Слева прямая скобка, справа – угловая, а между ними – идентификатор перспективы. А QS опишем как сумму всех перспектив, помноженных на свою амплитуду каждая:
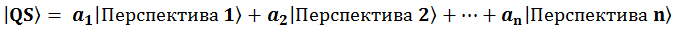
Числа 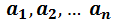 – это как раз амплитуды вероятности соответствующих перспектив. В общем случае это комплексные числа.
– это как раз амплитуды вероятности соответствующих перспектив. В общем случае это комплексные числа.
Продемонстрируем. Допустим, мы планируем измерить спин протона в Z-базисе (кто забыл, что такое «измерение в базисе», перечитайте главу 1). Тогда мы представим квантовое состояние, например, так:

Проговорим подробнее интерпретацию этой записи.
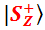 – так обозначена перспектива получить исход «плюс» при измерении спина в Z-базисе. Амплитуда этой перспективы равна
– так обозначена перспектива получить исход «плюс» при измерении спина в Z-базисе. Амплитуда этой перспективы равна 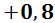 . Следовательно, вероятность реализации равна
. Следовательно, вероятность реализации равна 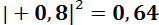 .
.
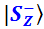 – перспектива получить при том же измерении «минус». У этой перспективы амплитуда равна
– перспектива получить при том же измерении «минус». У этой перспективы амплитуда равна 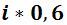 (комплексная единица, умноженная на ноль целых шесть десятых). Вероятность реализации
(комплексная единица, умноженная на ноль целых шесть десятых). Вероятность реализации 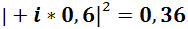 .
.
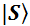 – собственно, спиновое QS. Формально мы это тоже можем понимать как перспективу, а именно – перспективу получить при измерении спина в Z-базисе хоть какой-нибудь исход. Амплитуда вероятности реализации этой «всеобъемлющей» перспективы, очевидно, равна единице, ведь какой-то из двух возможных исходов мы непременно получим.
– собственно, спиновое QS. Формально мы это тоже можем понимать как перспективу, а именно – перспективу получить при измерении спина в Z-базисе хоть какой-нибудь исход. Амплитуда вероятности реализации этой «всеобъемлющей» перспективы, очевидно, равна единице, ведь какой-то из двух возможных исходов мы непременно получим.
У вас может возникнуть вопрос: а почему мы записываем QS в виде суммы перспектив, а не в виде простого перечисления, как проделали чуть выше? Штука в том, что для описания чистых квантовых состояний прекрасно подходит векторный математический аппарат.
Чистое состояние
Пока что мы обсуждаем только чистые квантовые состояния. О том, чем отличаются чистое и смешанное состояние, мы поговорим дальше. Пока что положим так: чистое QS – это независимое QS. То есть, с одной стороны, любые манипуляции с изучаемой квантовой системой (в нашем случае это отдельный протон) не влияют на QS прочих квантовых систем (других протонов, например). И наоборот, любые манипуляции с прочими квантовыми системами не влияют на QS нашего протона.
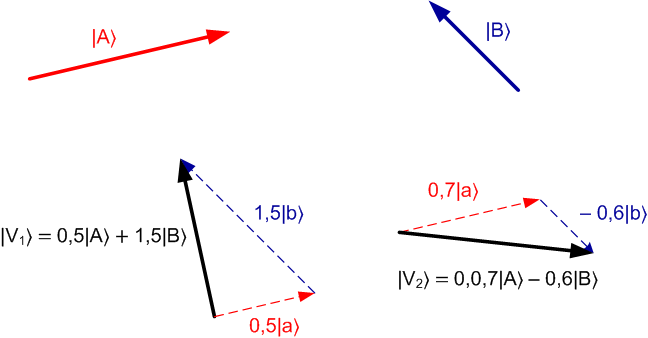
Я надеюсь, что читатель этой главы знаком с основами векторной алгебры (школьная математика), но всё же напомню одну из главных идей на примере двухмерного пространства – обычной декартовой плоскости. Возьмём два произвольных вектора, ненулевых и непараллельных друг другу, и объявим их в качестве базисных. Тогда любой другой вектор на этой плоскости можно представить как сумму базисных векторов, помноженных на определённый коэффициент каждый. Вот поясняющая картинка.
|
|
|
Рисунок 4-3 |
Пожалуйста, вектора 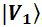 ,
, 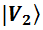 представлены через базисные вектора
представлены через базисные вектора 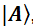 ,
, 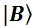 . Можно сказать и так: вектора
. Можно сказать и так: вектора 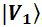 ,
, 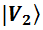 представлены в базисе
представлены в базисе 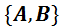 .
.
Обозначения
В школьном курсе математики, если кто помнит, вектора обозначают стрелочкой или полочкой поверх символа. Но я здесь сразу использовал обозначения, принятые в квантовой механике – символ между прямой и угловой скобкой.
Конечно, необходимое количество базисных векторов определяется размерностью пространства, в котором мы работаем. Так, для представления любого трёхмерного вектора понадобится три базисных вектора – это легко представить. Для четырёхмерного пространства нужно четыре базисных вектора, и так далее. Пространства размерности больше трёх невозможно представить себе, а тем более – изобразить на рисунке. Тем не менее, векторная формалистика позволяет с ними работать. Например, четырехмерный вектор будет точно также записываться в виде векторной суммы, только в ней будет уже четыре слагаемых.
Так вот, в математическом смысле каждую квантовую перспективу следует рассматривать как базисный вектор. А квантовое состояние – как векторную сумму перспектив, каждая со своим коэффициентом – амплитудой вероятности. Надо только чётко понимать, что речь здесь идёт не о привычных со школы векторах в физическом пространстве. Имеется в виду абстрактное математическое пространство, размерность которого определяется количеством возможных перспектив.
По-взрослому
Математики называют такую абстракцию «пространство Гильберта»
Это уже сильно высшая математика, но нам нет необходимости глубоко в неё погружаться. Просто знайте, что векторная алгебра прекрасно работает применительно к квантовым перспективам и даёт результаты, которые подтверждаются вполне конкретными экспериментами.
В формуле f.4-1 вектор квантового состояния 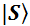 представлен через базисные состояния
представлен через базисные состояния 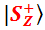 и
и 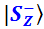 . Тот, у кого все эти векторные абстракции вызывают трудности, можем понимать формулу так: квантовое состояние
. Тот, у кого все эти векторные абстракции вызывают трудности, можем понимать формулу так: квантовое состояние 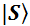 содержит в себе «кусочки» базисных состояний
содержит в себе «кусочки» базисных состояний 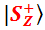 и
и 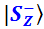 .
.
Модель
Аналогично тому, как перспектива «вытащить из лототрона шар какого угодно цвета» состоит из кусочков «базисных» перспектив «вытащить красный шар» и «вытащить синий шар». Базисным состояниями лототрона являются, понятное дело, расклады: «все красные» и «все синие».
Размер каждого «кусочка» определяется амплитудой вероятности – комплексным числом, стоящим в формуле перед вектором каждой перспективы. Повторим ещё раз, потому что очень важно: вероятность реализации перспективы легко вычислить, возведя модуль амплитуды вероятности в квадрат.
Закрепим понимание следующим. В главе 1 мы рассматривали ситуации, когда исход измерения спина однозначно предопределён. Пусть, например, для измерения в Z-базисе предопределён исход «плюс». Как математически описать такое квантовое состояние? Проще простого:
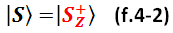
Вот, амплитуда перспективы получить при измерении исход «плюс» равна единице, амплитуда перспективы получить при измерении исход «минус» равна нулю. Это означает, что протон находится в базисном состоянии 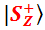 , которое в литературе принято ещё называть «спин вверх». В данном случае квантовое состояние
, которое в литературе принято ещё называть «спин вверх». В данном случае квантовое состояние 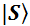 не содержит в себе ни малейшего кусочка базисного состояния
не содержит в себе ни малейшего кусочка базисного состояния 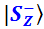 .
.
Обратите внимание, если бы мы подходили к вопросу совсем формально, указывая амплитуды всех возможных в данной ситуации базисных состояний, то нам следовало бы (f.4-2) написать так:
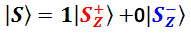
Но в сложившейся квантовой традиции перспективы с нулевой амплитудой включать в формулу QS не принято. И так понятно, что они при измерении «не играют».
А вот обратная ситуация, когда предопределён исход «минус», протон в базисном состоянии «спин вниз»:
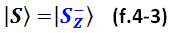
Это, как вы понимаете, крайние случаи полной предопределённости исхода измерения. Во всех других случаях QS записывается в виде суперпозиции (проще говоря – векторной суммы) базисных перспектив.