Шаг назад

Глава 5. Чистые, запутанные и смешанные (начало)

Перечисленные в предыдущей главе принципы являются универсальными и применимы для любых квантовых систем. Пока что мы делали упор на спине одиночной частицы, давайте же посмотрим теперь на системы, включающие несколько частиц.

Пусть у нас имеется два протона, условно – протоны A и B. Мы планируем измерить спин каждого из них, скажем, в Z-базисе, то есть, провести 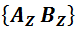измерение (о смысле такого обозначения мы договаривались во второй главе). В этом случае существует четыре потенциально возможных исхода, за которые «отвечают» четыре перспективы:

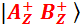 – оба измерения дадут «плюс»;

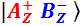 – измерение  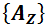даст «плюс», измерение  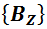даст «минус»,

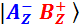 – измерение 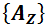даст «минус», измерение  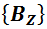даст «плюс»,

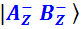 – оба измерения дадут «минус».

Правила математической «игры» здесь такие же, как в случае одиночного протона. Эти перспективы мы считаем базисными. А системное QS пары частиц опять представляем в виде векторной суммы базисных перспектив, каждая со своей амплитудой. Но в этом случае  в суперпозиции участвуют не два, а четыре слагаемых:  

Как и прежде, квадрат модуля амплитуды равен вероятности реализации  перспективы. Только здесь речь уже идёт о вероятности реализации той или иной комбинации двух исходов.

На всякий случай напомню, что если какие-то из амплитуд вероятности равны нулю, то соответствующие перспективы просто не записывают. Например, если бы нулю равнялись амплитуды a₁ и a₃ , то (f.5-1) мы записали бы в следующем виде:

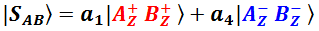
В таком QS реализуемы только те комбинации, в которых исходы одиночных измерени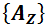й  и 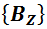 совпадают.

В ходе квантовых вычислений может возникнуть следующий вопрос. Вот есть у нас, допустим, два протона в системном состоянии вида (f.5-1). Какова вероятность того или иного исхода для первого одиночного измерения, например, протона B? Мы это легко вычислим. Достаточно просто сложить квадраты модулей амплитуд вероятности тех двойных перспектив, в которых измерение сулит одинаковый исход. В частности, для состояния (f.5-1), вероятность при измерении 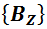 получить «плюс» будет равна:

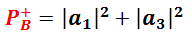
А вероятность при том же измерении получить «минус», очевидно, такова:

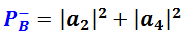
С тем, как надо понимать запись вида (f.5-1) всё понятно? Хорошо, теперь разберёмся с тем, как связаны одиночные QS отдельных протонов с системным QS пары. Самый простой случай – когда протоны A и B независимы. Иными словами, и протон A, и B находятся в чистом состоянии каждый. В этом случае исход измерения спина протона A не влияет на исход измерения спина B, и наоборот.

Пусть чистые состояния протонов таковы:

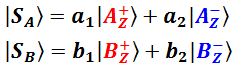
Как описать системное состояние такой пары? Надо просто перемножить 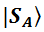 и 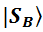. Ну как «просто»? Это ведь векторы, и речь, строго говоря, идёт о векторном произведении. Но нас тут такие тонкости могут не заботить, мы действуем так, как будто перемножаем две обычные скобки: 

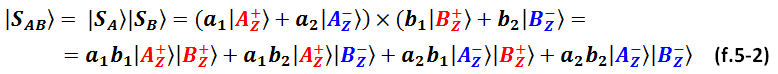
Логика такого произведения одиночных состояний аналогична той, которая используется при классических расчётах вероятности двойного события. Пусть у нас имеется два лототрона с красными и синими шарами, обозначим их тоже как A и B. И пусть вероятности исходов для лототронов таковы:

Для лототрона A:

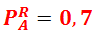 – вероятность вынуть красный шар;

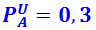 – вероятность вынуть синий шар;

Для лототрона B:

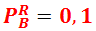 – вероятность вынуть красный шар;

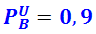 – вероятность вынуть синий шар;

Какова в таком случае вероятность, например, такой комбинации исходов: «вынуть красный из A и синий из B»? Она равна произведению вероятностей отдельных событий: «вынуть красный из A» и «вынуть синий из B»:

Так же и в формуле (f.5-2), только там, в силу квантовых особенностей, фигурируют не произведения вероятностей, а произведение амплитуд. Например, амплитуда перспективы получить два «плюса», обозначенной как 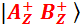, равна произведению амплитуд «одиночных» перспектив  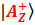и .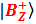

Кстати, запись вида 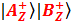 у нас будет означать то же самое, что и 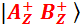, то есть, перспективу получения комбинации двух исходов. Аналогично и для комбинации трёх исходов.

Но любое ли системное квантовое состояние пары можно представить как комбинацию чистых квантовых состояний двух отдельных протонов? Отнюдь! Возьмём, например, пару в таком системном состоянии:

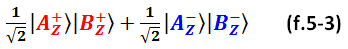
Это типичное белловское состояние ЭПР-пары, типа того, что было у нас в опыте на рисунке 2-1. Измерение спинов протонов A и B  в Z-базисе всегда дают одинаковый исход.

Невозможно представить это в виде произведения двух одиночных состояний (кто не верит – попробуйте). А это означает, что состояние каждого протона в ЭПР-паре не является чистым. Оно, что называется, смешанное. А системное состояние (f.5-3) называется запутанным. Полезно специально выделить следующее высказывание:

Квантовое состояние системы является смешанным, если она находится в запутанном состоянии с другой квантовой системой.

В примере, который мы сейчас рассматриваем, квантовые системы «протон А» и «протон B». находятся в смешанном QS каждая, потому что спины протонов запутаны друг с другом. Но отметим, что пара AB в целом находится хотя и в запутанном, но чистом квантовом состоянии.      

Дополнительная информация

Смешанное квантовое состояние невозможно представить в виде векторной суммы типа (f.4-1) или (f.5-1). Для его математического описания используется так называемая матрица плотности, доходчивый рассказ о которой оставим для будущих статей. 

Если каждый из протонов пары находится в чистом квантовом состоянии, то системное QS пары называют сепарабельным.

Таким образом, чистое QS (отдельной частицы или квантовой системы, состоящей из нескольких частиц) противопоставляется смешанному QS. В то время как сепарабельное QS (только квантовой системы) противопоставляется запутанному QS. Я сам раньше всё время с этими определениями путался, но вы теперь, надеюсь, не наступите на эти грабли.

Шаг вперёд